الجزائر
  1. الجزائر
  2. مقالات

قانون حجم الكرة في الرياضيات



قانون حجم الكرة في الرياضيات

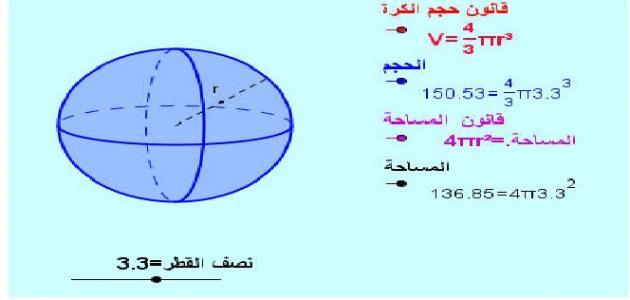
الكرة

تعريف الكرة

تُعرف الكرة على أنها مجموعة كل النقاط الموجودة في الفضاء الإقليدي ثلاثي الأبعاد والتي جميعها تبعد نفس المسافة عن نقطةٍ ما تُعرف بالمركز، كما تُعرف المسافة الفاصلة بين المركز وأي نقطة من النقاط المشكلة للكرة بنصف القطر، بينما القطر هو ضعف ، وهو يصل بين نقطتين متقابلتين على سطح هذه الكرة. ويوجد شرط حتى يتم اعتباره كرة، وهو أن يحقّق معادلة الكرة في المستوى الديكارتي.


قانون حجم الكرة

إن قانون حجم الكرة وهي معادلة الكرة في المستوى الديكارتي كالآتي:

س2+ص2+ز2= نق2
حيث إن "س"، "ص"، "ز" هي المحاور الثلاثة في المستوى الديكارتي ثلاثي الأبعاد، و"نق" هو نصف قطر هذه الكرة. ومن الجدير بالذكر أيضاً أن مقطع الكرة يمثل دائرة.


يوجد العديد من الأمور من المهم معرفتها حول الكرة، مثل حجمها ، ويمكن إيجاد حجم الكرة عن طريق العلاقة الآتية:

حجم الكرة = 3/4 نق3π
حيث إن "نق" هو نصف قطر الكرة، وπ هي الكسر 22/7 والذي يساوي تقريباً 3.14. ويمكن إيجاد عبر العلاقة الآتية:
مساحة سطح الكرة = 4 نق2π


أمثلة على حساب حجم الكرة

قانون حجم الكرة كما ذكرنا سابقاً هو 3/4×نق³×π، وفي هذا البند سوف نذكر العديد من الأمثلة التوضيحية على طريقة حساب حجم الكرة.

  • مثال (1): كرة نصف قطرها يساوي 5 سم، احسب حجمها.
الحلّ:
حجم الكرة = 3/4×نق³×π
= 3/4×5³×3.14
= 1570÷3
= 523.33 سم³.
  • مثال (2): كرة المضرب يصل طول قطرها إلى حوالي 3 سم، احسب حجمها.
الحلّ:
حجم الكرة = 3/4×نق³×π
= 3/4×3³×3.14
= 339.12 ÷ 3
= 113.04سم³.
  • مثال (3): إذا علمت أن حجم كرة يساوي 4220 سم³، احسب نصف قطر الكرة.
الحلّ:
حجم الكرة = 3/4×نق³×π
4220 = 3/4×نق³×3.14
4220= 12.56×نق³ /3
4220×3 = 12.53× نق³
نق³ = 12660÷12.56
≈ 1008
نق = الجذر التكعيبي ل 1008
= 10.03 سم.

مثال (4): إذا علمت أن مساحة كرة مطاطية للأطفال هي 1890 سم²، احسب حجم هذه الكرة.

الحلّ:
قانون مساحة الكرة = 4×نق²×π
1890 = 4×نق²×3.14
1890 = 12.56×نق²
ومنها نق² = 1890/ 12.56
نق² = 150.47
نق = الجذر التربيعي ل 150.47 = 12.26 سم.
الآن نستخدم قانون حجم الكرة
حجم الكرة = 3/4×نق³×ط
= 3/4×12.26³×3.14
= 23145.206÷3
= 7715.06 سم³.
  • مثال (5): إذا دارت دائرة حول أحد أقطارها لينتج شكل كرةٍ حجمها 1256سم³، احسب مساحة سطح هذه الكرة.
الحلّ:
لحساب مساحة سطح الكرة علينا أولاً إيجاد طول نصف قطرها.
حجم الكرة = 3/4×نق³×π
1256= 3/4×نق³×3.14
نق = 6.7 سم
مساحة الكرة = 4×نق²×π
= 4×نق³×3.14
= 3777.58 سم³.
  • مثال (6): كرة مساحتها 146سم³، احسب طول نصف قطرها.
الحلّ:
مساحة الكرة = 4×نق²×π
146 = 4×نق²×π
146 = 4×نق²×3.14 ومنها
نق² = 146/ 12.56
نق² = 11.62
نق = الجذر التربيعي ل 11.62 = 3.4 سم.
  • مثال (7): كرة حجمها 388ملم³، احسب مساحة ثلثي الكرة.
الحلّ:
لحساب مساحة ثلثي الكرة علينا أولاً إيجاد طول نصف قطرها، ولحساب مساحة ثلثيها نضرب المساحة الناتجة بالعدد 2/3.
حجم الكرة = 3/4×نق³×π
388 = 3/4×نق³×3.14
388 = 4.1866×نق³
نق³ = 388/4.1866
نق³ = 92.6766
نق = الجذر التكعيبي ل 92.6766
= 4.5253ملم
مساحة الكرة = 4×نق²×π
= 4×4.5253²×3.14
= 257.2079ملم³
مساحة ثلثي الكرة = مساحة الكرة×2/3
= 257.2079×2/3
= 171.47ملم³
  • مثال (8): لنفترض أن كروية الشكل تماماً، فإذا علمت أن نصف قطر الشمس هو 696,000 كيلومتر، أوجد حجم الشمس ثم قارنه بحجم إذا علمت أن نصف قطر الأرض (على اعتبار أنها كروية بشكل مثالي) هو 6,378 كيلومتراً.
الحل:
لإيجاد حجم الشمس سوف نستخدم علاقة لأننا اعتبرنا الشمس كرة بشكل مثالي،
حجم الشمس = 3/4×نق³×π
حجم الشمس = 3/4×(696000)³×π
حجم الشمس = 1.412 × 1018 كم3
وبنفس الطريقة يمكن إيجاد حجم الأرض،
حجم الأرض = 3/4×نق³×π
حجم الأرض = 3/4×(6378)³×π
حجم الأرض = 1.086 × 1012 كم3
من هذا المثال من الواضح أن الشمس أكبر من الأرض بحوالي مليون ضعف، ولو أخذنا النسبة بين حجم الشمس إلى حجم الأرض (أي قسمنا حجم الشمس على حجم ) سيكون بمقدورنا الاستنتاج أن الشمس تتسع ل 1،300،000 أرض (أي أنه يمكننا وضع مليون وثلاثمئة ألف أرض داخل الشمس).


معلومات إضافية عن الكرة

سابقاً تم توضيح طريقة حساب حجم الكرة عن طريق ذكر القانون المعني في حساب حجم الكرة، وإعطاء العديد من الأمثلة على طريقة حساب حجم الكرة، حيث إن الحجم هو عدد الوحدات المكعبة التي سوف تملأ الكرة. من الجدير بالذكر أيضاً هو أن الكمية 3/4×π تساوي تقريباً 4.19. ومن هذا يمكن القول إن حجم الكرة يساوي 4.19×نق3، وهذه العلاقة هي العلاقة التي توصل إليها أرخميدس قبل أكثر من ألفي عام، وكان قد توصل أيضاً إلى أن حجم الكرة يساوي تماماً ثلثي التي محيطها هو نفس محيط هذه الكرة (أي أصغر ممكن أن تحتوي الكرة).


يمكن قياس الحجم باستخدام مكعب (مكعب وحدات الطول يعني: وحدة طول × وحدة طول × وحدة طول)، ويمكن استخدام أي من الطول الموجودة في أي نظام لقياس الحجم طالما أن نصف القطر مقاس بنفس هذه الوحدة مثل المتر المكعب، والسنتيمتر المكعب، والميليمتر المكعب، والقدم المكعب، والإنش المكعب وغيرها (لاحظ أن وحدة نصف القطر سوف تكون متراً، ، وميليمتراً، وقدماً، ).






  1. تعليقكـم
سيظهر تعليقك على هذه الصفحة بعد موافقة المشرف.
هذا النمودج ليس مخصص لبعث رسالة شخصية لأين كان بل فضاء للنقاش و تبادل الآراء في إحترام
الاسم و اللقب :
البريد الالكتروني : *
المدينة : *
البلد : *
المهنة :
الرسالة : *
(الحقول المتبوعة بـ * إجبارية)